PointAnswers1: Difference between revisions

From WeBWorK_wiki
Jump to navigation Jump to search
(Created page with '<h2>Answer is a Point or a List of Points</h2> <p style="background-color:#eeeeee;border:black solid 1px;padding:3px;"> This PG code shows how to evaluate answers that are point…')
 
(add historical tag and give links to newer problems.)
 
(7 intermediate revisions by 3 users not shown)
Line 1: Line 1:
{{historical}}
<p style="font-size: 120%;font-weight:bold">This problem has been replaced with [https://openwebwork.github.io/pg-docs/sample-problems/Algebra/PointAnswers.html a newer version of this problem]</p>
<h2>Answer is a Point or a List of Points</h2>
<h2>Answer is a Point or a List of Points</h2>


<p style="background-color:#eeeeee;border:black solid 1px;padding:3px;">
[[File:PointAnswers1.png|300px|thumb|right|Click to enlarge]]
<p style="background-color:#f9f9f9;border:black solid 1px;padding:3px;">
This PG code shows how to evaluate answers that are points or lists of points.
This PG code shows how to evaluate answers that are points or lists of points.
<ul>
<li>Download file: [[File:PointAnswers1.txt]] (change the file extension from txt to pg when you save it)</li>
<li>File location in NPL: <code>NationalProblemLibrary/FortLewis/Authoring/Templates/Precalc/PointAnswers1.pg</code></li>
</ul>
</p>
</p>
* File location in OPL: [https://github.com/openwebwork/webwork-open-problem-library/blob/master/OpenProblemLibrary/FortLewis/Authoring/Templates/Precalc/PointAnswers1.pg FortLewis/Authoring/Templates/Precalc/PointAnswers1.pg]
* PGML location in OPL: [https://github.com/openwebwork/webwork-open-problem-library/blob/master/OpenProblemLibrary/FortLewis/Authoring/Templates/Precalc/PointAnswers1_PGML.pg FortLewis/Authoring/Templates/Precalc/PointAnswers1_PGML.pg]


<br clear="all" />
<p style="text-align:center;">
<p style="text-align:center;">
[[SubjectAreaTemplates|Templates by Subject Area]]
[[SubjectAreaTemplates|Templates by Subject Area]]
Line 16: Line 21:


<tr valign="top">
<tr valign="top">
<th> PG problem file </th>
<th style="width: 40%"> PG problem file </th>
<th> Explanation </th>
<th> Explanation </th>
</tr>
</tr>
Line 43: Line 48:


loadMacros(
loadMacros(
"PGstandard.pl",
  'PGstandard.pl',
"MathObjects.pl",
  'MathObjects.pl',
"contextLimitedPoint.pl",
  'contextLimitedPoint.pl',
  'PGML.pl',
  'PGcourse.pl'
);
);


Line 65: Line 72:
<td style="background-color:#ffffdd;border:black 1px dashed;">
<td style="background-color:#ffffdd;border:black 1px dashed;">
<pre>
<pre>
Context("LimitedPoint");
Context('LimitedPoint');


$f = Compute("x^2-1");
$f = Compute('x^2-1');


$xint = List( Point("(1,0)"), Point("(-1,0)") );
$xint = List( Point('(1,0)'), Point('(-1,0)') );
 
$yint = List( Point('(0,-1)') );
$yint = List( Point("(0,-1)") );
</pre>
</pre>
</td>
</td>
Line 81: Line 87:
points as if they were vectors).  The x-intercepts are clearly a
points as if they were vectors).  The x-intercepts are clearly a
list of points.  We used a list with only one element for the y-intercepts
list of points.  We used a list with only one element for the y-intercepts
so that a student who mistakenly enters two points will not get
so that a student who mistakenly enters two points will be told
a warning message.
their second point is incorrect.  If we did not use a list for
the y-intercepts, a student who enters two points would be given
an error message instead.
</p>
</p>
</td>
</td>
Line 92: Line 100:
<td style="background-color:#ffdddd;border:black 1px dashed;">
<td style="background-color:#ffdddd;border:black 1px dashed;">
<pre>
<pre>
Context()->texStrings;
BEGIN_PGML
BEGIN_TEXT
Enter the [`x`]-intercept(s) and [`y`]-intercept(s)
Enter the x-intercept(s) and y-intercept(s)
of [` y = [$f] `].  Enter a point as [` (a,b) `],
of \( y = $f \).  Enter a point as \( (a,b) \),
including the parentheses.  If there is more
including the parentheses.  If there is more  
than one correct answer, enter a comma
than one correct answer, enter a comma  
separated list of points.
separated list of points.
$BR
$BR
x-intercept(s): \{ ans_rule(20) \}
\{ AnswerFormatHelp("points") \}
$BR
y-intercept(s): \{ ans_rule(20) \}
\{ AnswerFormatHelp("points") \}
END_TEXT
Context()->normalStrings;
</pre>
<td style="background-color:#ffcccc;padding:7px;">
<p>
<b>Main Text:</b>
</p>
</td>
</tr>


<!-- Answer evaluation section -->
+ [`x`]-intercept(s): [_________________]{$xint}


<tr valign="top">
+ [`y`]-intercept(s): [_________________]{$yint}
<td style="background-color:#eeddff;border:black 1px dashed;">
<pre>
$showPartialCorrectAnswers = 1;


ANS( $xint->cmp() );
[@ helpLink('points') @]*
 
END_PGML
ANS( $yint->cmp() );
</pre>
</pre>
<td style="background-color:#eeccff;padding:7px;">
<td style="background-color:#ffcccc;padding:7px;">
<p>
<p>
<b>Answer Evaluation:</b>
<b>Main Text:</b>
Be sure to tell students the proper syntax for how to enter their answers.
</p>
</p>
</td>
</td>
Line 139: Line 127:
<td style="background-color:#ddddff;border:black 1px dashed;">
<td style="background-color:#ddddff;border:black 1px dashed;">
<pre>
<pre>
Context()->texStrings;
BEGIN_PGML_SOLUTION
BEGIN_SOLUTION
${PAR}SOLUTION:${PAR}
Solution explanation goes here.
Solution explanation goes here.
END_SOLUTION
END_PGML_SOLUTION
Context()->normalStrings;
 
COMMENT('MathObject version.');
 
ENDDOCUMENT();
ENDDOCUMENT();
</pre>
</pre>
Line 164: Line 146:


[[Category:Top]]
[[Category:Top]]
[[Category:Authors]]
[[Category:Sample Problems]]
[[Category:Subject Area Templates]]

Latest revision as of 10:08, 18 July 2023

This article has been retained as a historical document. It is not up-to-date and the formatting may be lacking. Use the information herein with caution.

This problem has been replaced with a newer version of this problem


Answer is a Point or a List of Points

Click to enlarge

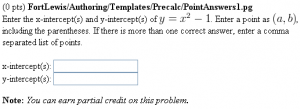
This PG code shows how to evaluate answers that are points or lists of points.


Templates by Subject Area

PG problem file Explanation

Problem tagging data

Problem tagging: 

DOCUMENT();

loadMacros(
  'PGstandard.pl',
  'MathObjects.pl',
  'contextLimitedPoint.pl',
  'PGML.pl',
  'PGcourse.pl'
);

TEXT(beginproblem());

Initialization: We only need to load contextLimitedPoint.pl if we want to prevent operations between points. 

Context('LimitedPoint');

$f = Compute('x^2-1');

$xint = List( Point('(1,0)'), Point('(-1,0)') );
$yint = List( Point('(0,-1)') );

Setup: We could have used Context("Point"); instead, which would allow mathematical operations between points (such as adding points as if they were vectors). The x-intercepts are clearly a list of points. We used a list with only one element for the y-intercepts so that a student who mistakenly enters two points will be told their second point is incorrect. If we did not use a list for the y-intercepts, a student who enters two points would be given an error message instead. 

BEGIN_PGML
Enter the [`x`]-intercept(s) and [`y`]-intercept(s)
of [` y = [$f] `].  Enter a point as [` (a,b) `],
including the parentheses.  If there is more
than one correct answer, enter a comma
separated list of points.

+ [`x`]-intercept(s): [_________________]{$xint}

+ [`y`]-intercept(s): [_________________]{$yint}

[@ helpLink('points') @]*
END_PGML

Main Text: Be sure to tell students the proper syntax for how to enter their answers. 

BEGIN_PGML_SOLUTION
Solution explanation goes here.
END_PGML_SOLUTION
ENDDOCUMENT();

Solution:

Templates by Subject Area

Retrieved from "https://wiki.openwebwork.org/index.php?title=PointAnswers1&oldid=23772"