PolarGraph1: Difference between revisions
(Created page with '<h2>Graphing a Parametric or Polar Curve</h2> 300px|thumb|right|Click to enlarge <p style="background-color:#f9f9f9;border:black solid 1px;padding:3px;"…') |
(add historical tag and give links to newer problems.) |
||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{historical}} | |||
<p style="font-size: 120%;font-weight:bold">This problem has been replaced with [https://openwebwork.github.io/pg-docs/sample-problems/Parametric/PolarGraph.html a newer version of this problem]</p> | |||
<h2>Graphing a Parametric or Polar Curve</h2> | <h2>Graphing a Parametric or Polar Curve</h2> | ||
[[File:PolarGraph1.png|300px|thumb|right|Click to enlarge]] | [[File:PolarGraph1.png|300px|thumb|right|Click to enlarge]] | ||
<p style="background-color:#f9f9f9;border:black solid 1px;padding:3px;"> | <p style="background-color:#f9f9f9;border:black solid 1px;padding:3px;"> | ||
This PG code shows how to . | This PG code shows how to graph a parametric curve or polar curve with a shading (a filled region). | ||
</p> | </p> | ||
* | * File location in OPL: [https://github.com/openwebwork/webwork-open-problem-library/blob/master/OpenProblemLibrary/FortLewis/Authoring/Templates/Parametric/PolarGraph1.pg FortLewis/Authoring/Templates/Parametric/PolarGraph1.pg] | ||
* | * PGML location in OPL: [https://github.com/openwebwork/webwork-open-problem-library/blob/master/OpenProblemLibrary/FortLewis/Authoring/Templates/Parametric/PolarGraph1_PGML.pg FortLewis/Authoring/Templates/Parametric/PolarGraph1_PGML.pg] | ||
<br clear="all" /> | <br clear="all" /> | ||
| Line 97: | Line 101: | ||
$f->domain(0,3.14); | $f->domain(0,3.14); | ||
$f->steps(90); | $f->steps(90); | ||
$f->weight(2); | |||
$f->color('darkgreen'); | $f->color('darkgreen'); | ||
$gr->fillRegion([0.5,0.1,'lightgreen']); | $gr->fillRegion([0.5,0.1,'lightgreen']); | ||
| Line 106: | Line 110: | ||
<p> | <p> | ||
<b>Setup:</b> | <b>Setup:</b> | ||
We initialize a graph object named <code>$gr</code>. We define several new named colors which you can use if you want. We construct MathObjects formulas <code>$x</code> and <code>$y</code> for the x- and y-coordinates in terms of the parameter t. Then, we pass these formulas to the <code>Fun</code> routine, converting them to perl subroutines via <code>->perlFunction</code>, and attach them to the graph object <code>$gr</code>. Then, we set some of the options for the graph of the parametric curve <code>$f</code>. Finally, we fill the region enclosing the point <code>(0.5,0.1)</code> with the color light green. | |||
</p> | </p> | ||
</td> | </td> | ||
| Line 142: | Line 147: | ||
<p> | <p> | ||
<b>Main Text:</b> | <b>Main Text:</b> | ||
We use the <code>ColumnTable(column 1, column 2, options)</code> to put the text and graph side-by-side. We join (Perl) strings <code>" "</code> to common PG commands like <code>ans_rule(20)</code> using the string concatenation operator <code> . </code> which is a period. Notice that the commas between column 1, column 2, and the options do not have any periods before them. | |||
</p> | </p> | ||
</td> | </td> | ||
| Line 170: | Line 176: | ||
Context()->texStrings; | Context()->texStrings; | ||
BEGIN_SOLUTION | BEGIN_SOLUTION | ||
Solution explanation goes here. | Solution explanation goes here. | ||
END_SOLUTION | END_SOLUTION | ||
| Line 193: | Line 198: | ||
[[Category:Top]] | [[Category:Top]] | ||
[[Category: | [[Category:Sample Problems]] | ||
[[Category:Subject Area Templates]] | |||
Latest revision as of 10:19, 18 July 2023
This problem has been replaced with a newer version of this problem
Graphing a Parametric or Polar Curve
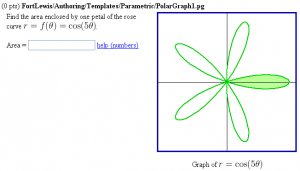
This PG code shows how to graph a parametric curve or polar curve with a shading (a filled region).
- File location in OPL: FortLewis/Authoring/Templates/Parametric/PolarGraph1.pg
- PGML location in OPL: FortLewis/Authoring/Templates/Parametric/PolarGraph1_PGML.pg
| PG problem file | Explanation |
|---|---|
|
Problem tagging: |
|
DOCUMENT(); loadMacros( "PGstandard.pl", "MathObjects.pl", "PGgraphmacros.pl", "AnswerFormatHelp.pl", "unionTables.pl", ); TEXT(beginproblem()); $refreshCachedImages = 1; |
Initialization:
We use |
Context("Numeric")->variables->are(t=>"Real");
$gr = init_graph(-1.1,-1.1,1.1,1.1,axes=>[0,0],size=>[300,300]);
#
# Define some useful colors
#
$gr->new_color("lightblue", 198,217,253); # RGB
$gr->new_color("darkblue", 77,137,249);
$gr->new_color("lightred", 255,127,127);
$gr->new_color("darkred", 255, 55, 55);
$gr->new_color("lightorange", 255,204,127);
$gr->new_color("darkorange", 255, 153, 0);
$gr->new_color("lightgreen", 187, 255, 153);
$gr->new_color("darkgreen", 0, 208, 0);
#
# For a polar curve r = f(t),
# x = r cos(t) = f(t) cos(t)
# y = r sin(t) = f(t) sin(t)
#
$x = Formula("cos(5*t) * cos(t)");
$y = Formula("cos(5*t) * sin(t)");
$f = new Fun( $x->perlFunction, $y->perlFunction, $gr );
$f->domain(0,3.14);
$f->steps(90);
$f->weight(2);
$f->color('darkgreen');
$gr->fillRegion([0.5,0.1,'lightgreen']);
|
Setup:
We initialize a graph object named |
Context()->texStrings;
BEGIN_TEXT
\{
ColumnTable(
"Find the area enclosed by one petal of the
rose curve \( r = f(\theta) = \cos(5\theta) \).
$BR
$BR
Area = ".
ans_rule(20).$SPACE.
AnswerFormatHelp("numbers")
,
$BCENTER.
image( insertGraph($gr), width=>300, height=>300 ).
$PAR.
"Graph of \( r = \cos(5\theta) \)".
$ECENTER
,
indent => 0, separation => 30, valign => "TOP"
);
\}
END_TEXT
Context()->normalStrings;
|
Main Text:
We use the |
$showPartialCorrectAnswers = 1;
# intentionally incorrect
ANS( Compute("pi")->cmp() );
|
Answer Evaluation: |
Context()->texStrings;
BEGIN_SOLUTION
Solution explanation goes here.
END_SOLUTION
Context()->normalStrings;
COMMENT('MathObject version.');
ENDDOCUMENT();
|
Solution: |