DoubleIntegral1: Difference between revisions
Paultpearson (talk | contribs) (PGML example link) |
(add historical tag and give links to newer problems.) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{historical}} | |||
<p style="font-size: 120%;font-weight:bold">This problem has been replaced with [https://openwebwork.github.io/pg-docs/sample-problems/IntegralCalc/DoubleIntegral.html a newer version of this problem]</p> | |||
<h2>Setting up a Double Integral</h2> | <h2>Setting up a Double Integral</h2> | ||
| Line 5: | Line 9: | ||
This PG code shows how to allow students to set up a double integral and integrate in either order. | This PG code shows how to allow students to set up a double integral and integrate in either order. | ||
</p> | </p> | ||
* File location in OPL: [https://github.com/openwebwork/webwork-open-problem-library/blob/master/OpenProblemLibrary/FortLewis/Authoring/Templates/IntegralCalcMV/DoubleIntegral1.pg FortLewis/Authoring/Templates/IntegralCalcMV/DoubleIntegral1.pg] | <!-- * File location in OPL: [https://github.com/openwebwork/webwork-open-problem-library/blob/master/OpenProblemLibrary/FortLewis/Authoring/Templates/IntegralCalcMV/DoubleIntegral1.pg FortLewis/Authoring/Templates/IntegralCalcMV/DoubleIntegral1.pg] --> | ||
* PGML location in OPL: [https://github.com/openwebwork/webwork-open-problem-library/blob/master/OpenProblemLibrary/FortLewis/Authoring/Templates/IntegralCalcMV/DoubleIntegral1_PGML.pg FortLewis/Authoring/Templates/IntegralCalcMV/DoubleIntegral1_PGML.pg] | * PGML location in OPL: [https://github.com/openwebwork/webwork-open-problem-library/blob/master/OpenProblemLibrary/FortLewis/Authoring/Templates/IntegralCalcMV/DoubleIntegral1_PGML.pg FortLewis/Authoring/Templates/IntegralCalcMV/DoubleIntegral1_PGML.pg] | ||
| Line 16: | Line 20: | ||
<tr valign="top"> | <tr valign="top"> | ||
<th> PG problem file </th> | <th style="width: 50%"> PG problem file </th> | ||
<th> Explanation </th> | <th> Explanation </th> | ||
</tr> | </tr> | ||
| Line 65: | Line 69: | ||
<td style="background-color:#ffffdd;border:black 1px dashed;"> | <td style="background-color:#ffffdd;border:black 1px dashed;"> | ||
<pre> | <pre> | ||
Context( | Context('Numeric'); | ||
Context()->variables->are( | Context()->variables->are( | ||
x=> | x => 'Real', | ||
y=> | dx => 'Real', | ||
Context()->flags->set(reduceConstants=>0); | y => 'Real', | ||
dy => 'Real' | |||
); | |||
Context()->flags->set(reduceConstants => 0); | |||
# | # | ||
# limits of integration | # limits of integration | ||
# | # | ||
$a = random(1,5,1); | $a = random(1, 5, 1); | ||
$b = $a + random(1,4,1); | $b = $a + random(1, 4, 1); | ||
do { $c = random(1,5,1); } until ($c != $a); | do { $c = random(1, 5, 1); } until ($c != $a); | ||
do { $d = $c + random(1,4,1); } until ($d != $b); | do { $d = $c + random(1, 4, 1); } until ($d != $b); | ||
# | # | ||
# integrand and volume | # integrand and volume | ||
# | # | ||
$f = Formula( | $f = Formula('x*y'); | ||
$V = Formula("($b^2-$a^2) * ($d^2-$c^2) / 4"); | $V = Formula("($b^2-$a^2) * ($d^2-$c^2) / 4"); | ||
# | # | ||
# differentials and limits of integration | # differentials and limits of integration | ||
# | # | ||
# Case 0, element 0 of each array below, is | # Case 0, element 0 of each array below, is | ||
# if the order of integration is dx dy | # if the order of integration is dx dy | ||
# | # | ||
# Case 1, element 1 of each array below, is | # Case 1, element 1 of each array below, is | ||
# if the order of integration is dy dx | # if the order of integration is dy dx | ||
# | # | ||
@id = (Formula( | # 'id' and 'od' stand for inner and outer differential | ||
@od = (Formula( | # | ||
@id = (Formula('dx'), Formula('dy')); # (case 0, case 1) | |||
@od = (Formula('dy'), Formula('dx')); # (case 0, case 1) | |||
# | # | ||
# A = outer integral, lower limit | # A = outer integral, lower limit | ||
| Line 105: | Line 111: | ||
# D = inner integral, upper limit | # D = inner integral, upper limit | ||
# | # | ||
@A = (Formula("$c"),Formula("$a")); # (case 0, case 1) | @A = (Formula("$c"), Formula("$a")); # (case 0, case 1) | ||
@B = (Formula("$d"),Formula("$b")); # (case 0, case 1) | @B = (Formula("$d"), Formula("$b")); # (case 0, case 1) | ||
@C = (Formula("$a"),Formula("$c")); # (case 0, case 1) | @C = (Formula("$a"), Formula("$c")); # (case 0, case 1) | ||
@D = (Formula("$b"),Formula("$d")); # (case 0, case 1) | @D = (Formula("$b"), Formula("$d")); # (case 0, case 1) | ||
$multians = MultiAnswer( $f, $id[0], $od[0], $A[0], $B[0], $C[0], $D[0] )->with( | $multians = MultiAnswer($f, $id[0], $od[0], $A[0], $B[0], $C[0], $D[0])->with( | ||
singleResult => 1, | |||
checker => sub { | |||
my ($correct, $student, $self) = @_; | |||
my ($fstu, $idstu, $odstu, $Astu, $Bstu, $Cstu, $Dstu) = @{$student}; | |||
if ( | |||
( | |||
$f == $fstu | |||
&& $id[0] == $idstu | |||
&& $od[0] == $odstu | |||
&& $A[0] == $Astu | |||
&& $B[0] == $Bstu | |||
&& $C[0] == $Cstu | |||
&& $D[0] == $Dstu | |||
) | |||
|| ($f == $fstu | |||
&& $id[1] == $idstu | |||
&& $od[1] == $odstu | |||
&& $A[1] == $Astu | |||
&& $B[1] == $Bstu | |||
&& $C[1] == $Cstu | |||
&& $D[1] == $Dstu) | |||
) | |||
{ | |||
return 1; | |||
} elsif ( | |||
( | |||
$f == $fstu | |||
&& $id[0] == $idstu | |||
&& $od[0] == $odstu | |||
&& ($A[0] != $Astu || $B[0] != $Bstu) | |||
&& $C[0] == $Cstu | |||
&& $D[0] == $Dstu | |||
) | |||
|| ($f == $fstu | |||
&& $id[1] == $idstu | |||
&& $od[1] == $odstu | |||
&& ($A[1] != $Astu || $B[1] != $Bstu) | |||
&& $C[1] == $Cstu | |||
&& $D[1] == $Dstu) | |||
|| ($f == $fstu | |||
&& $id[0] == $idstu | |||
&& $od[0] == $odstu | |||
&& $A[0] == $Astu | |||
&& $B[0] == $Bstu | |||
&& ($C[0] != $Cstu || $D[0] != $Dstu)) | |||
|| ($f == $fstu | |||
&& $id[1] == $idstu | |||
&& $od[1] == $odstu | |||
&& $A[1] == $Astu | |||
&& $B[1] == $Bstu | |||
&& ($C[1] != $Cstu || $D[1] != $Dstu)) | |||
) | |||
{ | |||
$self->setMessage(1, 'Check your limits of integration.'); | |||
return 0.94; | |||
} elsif ( | |||
( | |||
$f == $fstu | |||
&& $id[0] == $idstu | |||
&& $od[0] == $odstu | |||
&& ($A[0] != $Astu || $B[0] != $Bstu) | |||
&& ($C[0] != $Cstu || $D[0] != $Dstu) | |||
) | |||
|| ($f == $fstu | |||
&& $id[1] == $idstu | |||
&& $od[1] == $odstu | |||
&& ($A[1] != $Astu || $B[1] != $Bstu) | |||
&& ($C[1] != $Cstu || $D[1] != $Dstu)) | |||
) | |||
{ | |||
$self->setMessage(1, 'Check your limits of integration and order of integration.'); | |||
return 0.47; | |||
} else { | |||
return 0; | |||
} | |||
} | |||
); | ); | ||
</pre> | </pre> | ||
| Line 220: | Line 212: | ||
<td style="background-color:#ffdddd;border:black 1px dashed;"> | <td style="background-color:#ffdddd;border:black 1px dashed;"> | ||
<pre> | <pre> | ||
BEGIN_PGML | |||
Set up a double integral in rectangular coordinates | Set up a double integral in rectangular coordinates | ||
for calculating the volume of the solid under the | for calculating the volume of the solid under the | ||
graph of the function | graph of the function [` f(x,y) = [$f] `] over the | ||
region | region [` [$a] \leq x \leq [$b] `] and [` [$c] \leq y \leq [$d] `]. | ||
_Instructions:_ | |||
Please enter the integrand in the first answer box. | |||
Please enter the integrand in the first answer box. | Depending on the order of integration you choose, | ||
Depending on the order of integration you choose, | enter _dx_ and _dy_ | ||
enter | in either order into the second and third answer boxes | ||
in either order into the second and third answer boxes | with only one _dx_ or _dy_ in each box. | ||
with only one | Then, enter the limits of | ||
integration and evaluate the integral to find the volume. | |||
integration and evaluate the integral to find the volume. | |||
[`` \int_A^B \int_C^D ``] | |||
[___________]{$multians} [_____]{$multians} [_____]{$multians} | |||
A = [_____________]{$multians} | |||
B = [_____________]{$multians} | |||
C = [_____________]{$multians} | |||
$ | D = [_____________]{$multians} | ||
Volume = [___________________________]{$V} | |||
</pre> | </pre> | ||
<td style="background-color:# | <td style="background-color:#ffcccc;padding:7px;"> | ||
<p> | <p> | ||
<b> | <b>Main Text:</b> | ||
The only interesting thing to note here is that you must use <code>$multians</code> for each answer blank (except the last one, which is independent.) | |||
</p> | </p> | ||
</td> | </td> | ||
| Line 284: | Line 250: | ||
<td style="background-color:#ddddff;border:black 1px dashed;"> | <td style="background-color:#ddddff;border:black 1px dashed;"> | ||
<pre> | <pre> | ||
BEGIN_PGML_SOLUTION | |||
Solution explanation goes here. | Solution explanation goes here. | ||
END_PGML_SOLUTION | |||
COMMENT(' | COMMENT('Allows integration in either order. Uses PGML.'); | ||
ENDDOCUMENT(); | ENDDOCUMENT(); | ||
</pre> | </pre> | ||
Latest revision as of 10:29, 18 July 2023
This problem has been replaced with a newer version of this problem
Setting up a Double Integral
This PG code shows how to allow students to set up a double integral and integrate in either order.
- PGML location in OPL: FortLewis/Authoring/Templates/IntegralCalcMV/DoubleIntegral1_PGML.pg
| PG problem file | Explanation |
|---|---|
|
Problem tagging: |
|
DOCUMENT(); loadMacros( "PGstandard.pl", "MathObjects.pl", "parserMultiAnswer.pl", ); TEXT(beginproblem()); |
Initialization:
Since there are multiple answer blanks that are dependent upon each other, we use |
Context('Numeric');
Context()->variables->are(
x => 'Real',
dx => 'Real',
y => 'Real',
dy => 'Real'
);
Context()->flags->set(reduceConstants => 0);
#
# limits of integration
#
$a = random(1, 5, 1);
$b = $a + random(1, 4, 1);
do { $c = random(1, 5, 1); } until ($c != $a);
do { $d = $c + random(1, 4, 1); } until ($d != $b);
#
# integrand and volume
#
$f = Formula('x*y');
$V = Formula("($b^2-$a^2) * ($d^2-$c^2) / 4");
#
# differentials and limits of integration
#
# Case 0, element 0 of each array below, is
# if the order of integration is dx dy
#
# Case 1, element 1 of each array below, is
# if the order of integration is dy dx
#
# 'id' and 'od' stand for inner and outer differential
#
@id = (Formula('dx'), Formula('dy')); # (case 0, case 1)
@od = (Formula('dy'), Formula('dx')); # (case 0, case 1)
#
# A = outer integral, lower limit
# B = outer integral, upper limit
# C = inner integral, lower limit
# D = inner integral, upper limit
#
@A = (Formula("$c"), Formula("$a")); # (case 0, case 1)
@B = (Formula("$d"), Formula("$b")); # (case 0, case 1)
@C = (Formula("$a"), Formula("$c")); # (case 0, case 1)
@D = (Formula("$b"), Formula("$d")); # (case 0, case 1)
$multians = MultiAnswer($f, $id[0], $od[0], $A[0], $B[0], $C[0], $D[0])->with(
singleResult => 1,
checker => sub {
my ($correct, $student, $self) = @_;
my ($fstu, $idstu, $odstu, $Astu, $Bstu, $Cstu, $Dstu) = @{$student};
if (
(
$f == $fstu
&& $id[0] == $idstu
&& $od[0] == $odstu
&& $A[0] == $Astu
&& $B[0] == $Bstu
&& $C[0] == $Cstu
&& $D[0] == $Dstu
)
|| ($f == $fstu
&& $id[1] == $idstu
&& $od[1] == $odstu
&& $A[1] == $Astu
&& $B[1] == $Bstu
&& $C[1] == $Cstu
&& $D[1] == $Dstu)
)
{
return 1;
} elsif (
(
$f == $fstu
&& $id[0] == $idstu
&& $od[0] == $odstu
&& ($A[0] != $Astu || $B[0] != $Bstu)
&& $C[0] == $Cstu
&& $D[0] == $Dstu
)
|| ($f == $fstu
&& $id[1] == $idstu
&& $od[1] == $odstu
&& ($A[1] != $Astu || $B[1] != $Bstu)
&& $C[1] == $Cstu
&& $D[1] == $Dstu)
|| ($f == $fstu
&& $id[0] == $idstu
&& $od[0] == $odstu
&& $A[0] == $Astu
&& $B[0] == $Bstu
&& ($C[0] != $Cstu || $D[0] != $Dstu))
|| ($f == $fstu
&& $id[1] == $idstu
&& $od[1] == $odstu
&& $A[1] == $Astu
&& $B[1] == $Bstu
&& ($C[1] != $Cstu || $D[1] != $Dstu))
)
{
$self->setMessage(1, 'Check your limits of integration.');
return 0.94;
} elsif (
(
$f == $fstu
&& $id[0] == $idstu
&& $od[0] == $odstu
&& ($A[0] != $Astu || $B[0] != $Bstu)
&& ($C[0] != $Cstu || $D[0] != $Dstu)
)
|| ($f == $fstu
&& $id[1] == $idstu
&& $od[1] == $odstu
&& ($A[1] != $Astu || $B[1] != $Bstu)
&& ($C[1] != $Cstu || $D[1] != $Dstu))
)
{
$self->setMessage(1, 'Check your limits of integration and order of integration.');
return 0.47;
} else {
return 0;
}
}
);
|
Setup:
There are two separate cases: integrating with respect to
The |
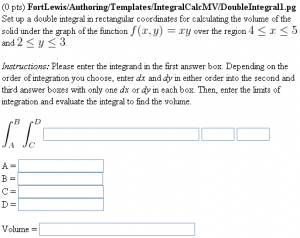
BEGIN_PGML
Set up a double integral in rectangular coordinates
for calculating the volume of the solid under the
graph of the function [` f(x,y) = [$f] `] over the
region [` [$a] \leq x \leq [$b] `] and [` [$c] \leq y \leq [$d] `].
_Instructions:_
Please enter the integrand in the first answer box.
Depending on the order of integration you choose,
enter _dx_ and _dy_
in either order into the second and third answer boxes
with only one _dx_ or _dy_ in each box.
Then, enter the limits of
integration and evaluate the integral to find the volume.
[`` \int_A^B \int_C^D ``]
[___________]{$multians} [_____]{$multians} [_____]{$multians}
A = [_____________]{$multians}
B = [_____________]{$multians}
C = [_____________]{$multians}
D = [_____________]{$multians}
Volume = [___________________________]{$V}
|
Main Text:
The only interesting thing to note here is that you must use |
BEGIN_PGML_SOLUTION
Solution explanation goes here.
END_PGML_SOLUTION
COMMENT('Allows integration in either order. Uses PGML.');
ENDDOCUMENT();
|
Solution: |