PointAnswers1: Difference between revisions

From WeBWorK_wiki
Jump to navigation Jump to search
(PGML example link)
(Removes the AnswerFormatHelp macro and some other cleanup.)
Line 16: Line 16:


<tr valign="top">
<tr valign="top">
<th> PG problem file </th>
<th style="width: 40%"> PG problem file </th>
<th> Explanation </th>
<th> Explanation </th>
</tr>
</tr>
Line 43: Line 43:


loadMacros(
loadMacros(
"PGstandard.pl",
  'PGstandard.pl',
"MathObjects.pl",
  'MathObjects.pl',
"AnswerFormatHelp.pl",
  'contextLimitedPoint.pl',
"contextLimitedPoint.pl",
  'PGML.pl',
  'PGcourse.pl'
);
);


Line 66: Line 67:
<td style="background-color:#ffffdd;border:black 1px dashed;">
<td style="background-color:#ffffdd;border:black 1px dashed;">
<pre>
<pre>
Context("LimitedPoint");
Context('LimitedPoint');


$f = Compute("x^2-1");
$f = Compute('x^2-1');


$xint = List( Point("(1,0)"), Point("(-1,0)") );
$xint = List( Point('(1,0)'), Point('(-1,0)') );
 
$yint = List( Point('(0,-1)') );
$yint = List( Point("(0,-1)") );
</pre>
</pre>
</td>
</td>
Line 95: Line 95:
<td style="background-color:#ffdddd;border:black 1px dashed;">
<td style="background-color:#ffdddd;border:black 1px dashed;">
<pre>
<pre>
Context()->texStrings;
BEGIN_PGML
BEGIN_TEXT
Enter the [`x`]-intercept(s) and [`y`]-intercept(s)
Enter the x-intercept(s) and y-intercept(s)
of [` y = [$f] `].  Enter a point as [` (a,b) `],
of \( y = $f \).  Enter a point as \( (a,b) \),
including the parentheses.  If there is more
including the parentheses.  If there is more  
than one correct answer, enter a comma
than one correct answer, enter a comma  
separated list of points.
separated list of points.
$BR
 
$BR
+ [`x`]-intercept(s): [_________________]{$xint}
x-intercept(s): \{ ans_rule(20) \}
 
\{ AnswerFormatHelp("points") \}
+ [`y`]-intercept(s): [_________________]{$yint}
$BR
 
y-intercept(s): \{ ans_rule(20) \}
[@ helpLink('points') @]*
\{ AnswerFormatHelp("points") \}
END_PGML
END_TEXT
Context()->normalStrings;
</pre>
</pre>
<td style="background-color:#ffcccc;padding:7px;">
<td style="background-color:#ffcccc;padding:7px;">
Line 116: Line 113:
<b>Main Text:</b>
<b>Main Text:</b>
Be sure to tell students the proper syntax for how to enter their answers.
Be sure to tell students the proper syntax for how to enter their answers.
</p>
</td>
</tr>
<!-- Answer evaluation section -->
<tr valign="top">
<td style="background-color:#eeddff;border:black 1px dashed;">
<pre>
$showPartialCorrectAnswers = 1;
ANS( $xint->cmp() );
ANS( $yint->cmp() );
</pre>
<td style="background-color:#eeccff;padding:7px;">
<p>
<b>Answer Evaluation:</b>
</p>
</p>
</td>
</td>
Line 143: Line 122:
<td style="background-color:#ddddff;border:black 1px dashed;">
<td style="background-color:#ddddff;border:black 1px dashed;">
<pre>
<pre>
Context()->texStrings;
BEGIN_PGML_SOLUTION
BEGIN_SOLUTION
${PAR}SOLUTION:${PAR}
Solution explanation goes here.
Solution explanation goes here.
END_SOLUTION
END_PGML_SOLUTION
Context()->normalStrings;
 
COMMENT('MathObject version.');
 
ENDDOCUMENT();
ENDDOCUMENT();
</pre>
</pre>

Revision as of 18:04, 10 March 2023

Answer is a Point or a List of Points

Click to enlarge

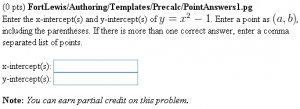
This PG code shows how to evaluate answers that are points or lists of points.


Templates by Subject Area

PG problem file Explanation

Problem tagging data

Problem tagging: 

DOCUMENT();

loadMacros(
  'PGstandard.pl',
  'MathObjects.pl',
  'contextLimitedPoint.pl',
  'PGML.pl',
  'PGcourse.pl'
);

TEXT(beginproblem());

Initialization: We only need to load contextLimitedPoint.pl if we want to prevent operations between points. 

Context('LimitedPoint');

$f = Compute('x^2-1');

$xint = List( Point('(1,0)'), Point('(-1,0)') );
$yint = List( Point('(0,-1)') );

Setup: We could have used Context("Point"); instead, which would allow mathematical operations between points (such as adding points as if they were vectors). The x-intercepts are clearly a list of points. We used a list with only one element for the y-intercepts so that a student who mistakenly enters two points will be told their second point is incorrect. If we did not use a list for the y-intercepts, a student who enters two points would be given an error message instead. 

BEGIN_PGML
Enter the [`x`]-intercept(s) and [`y`]-intercept(s)
of [` y = [$f] `].  Enter a point as [` (a,b) `],
including the parentheses.  If there is more
than one correct answer, enter a comma
separated list of points.

+ [`x`]-intercept(s): [_________________]{$xint}

+ [`y`]-intercept(s): [_________________]{$yint}

[@ helpLink('points') @]*
END_PGML

Main Text: Be sure to tell students the proper syntax for how to enter their answers. 

BEGIN_PGML_SOLUTION
Solution explanation goes here.
END_PGML_SOLUTION
ENDDOCUMENT();

Solution:

Templates by Subject Area

Retrieved from "https://wiki.openwebwork.org/index.php?title=PointAnswers1&oldid=23442"