RecursiveSequence1: Difference between revisions
m (moved Sequences1 to RecursiveSequence1) |
No edit summary |
||
| Line 1: | Line 1: | ||
<h2>Sequences and Recursively Defined Functions</h2> | <h2>Sequences and Recursively Defined Functions</h2> | ||
[[File: | [[File:RecursiveSequence1.png|300px|thumb|right|Click to enlarge]] | ||
<p style="background-color:#f9f9f9;border:black solid 1px;padding:3px;"> | <p style="background-color:#f9f9f9;border:black solid 1px;padding:3px;"> | ||
This PG code shows how to add a named function to the context and use it to ask students to come up with a recursive formula. | This PG code shows how to add a named function to the context and use it to ask students to come up with a recursive formula. | ||
</p> | </p> | ||
* Download file: [[File: | * Download file: [[File:RecursiveSequence1.txt]] (change the file extension from txt to pg when you save it) | ||
* File location in NPL: <code>FortLewis/Authoring/Templates/Sequences/ | * File location in NPL: <code>FortLewis/Authoring/Templates/Sequences/RecursiveSequence1.pg</code> | ||
Revision as of 23:09, 5 December 2010
Sequences and Recursively Defined Functions
This PG code shows how to add a named function to the context and use it to ask students to come up with a recursive formula.
- Download file: File:RecursiveSequence1.txt (change the file extension from txt to pg when you save it)
- File location in NPL:
FortLewis/Authoring/Templates/Sequences/RecursiveSequence1.pg
| PG problem file | Explanation |
|---|---|
|
Problem tagging: |
|
DOCUMENT(); loadMacros( "PGstandard.pl", "MathObjects.pl", "parserFunction.pl", ); TEXT(beginproblem()); |
Initialization:
We will be defining a new named function and adding it to the context, and the easiest way to do this is using |
Context("Numeric")->variables->are(n=>"Real");
parserFunction(f => "sin(pi^n)+e");
$fn = Formula("3 f(n-1) + 2");
|
Setup:
We define a new named function |
Context()->texStrings;
BEGIN_TEXT
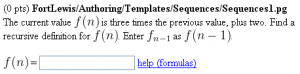
The current value \( f(n) \) is three
times the previous value, plus two. Find
a recursive definition for \( f(n) \).
Enter \( f_{n-1} \) as \( f(n-1) \).
$BR
\( f(n) \) = \{ ans_rule(20) \}
END_TEXT
Context()->normalStrings;
|
Main Text: We should tell students to use function notation rather than subscript notation so that they aren't confused about syntax. |
$showPartialCorrectAnswers=1; ANS( $fn->cmp() ); |
Answer Evaluation: |
Context()->texStrings;
BEGIN_SOLUTION
${PAR}SOLUTION:${PAR}
Solution explanation goes here.
END_SOLUTION
Context()->normalStrings;
COMMENT('MathObject version.');
ENDDOCUMENT();
|
Solution: |